一、矩阵分解概述

　　我们都知道，现实生活中的User-Item矩阵极大(User数量极大、Item数量极大)，而用户的兴趣和消费能力有限，对单个用户来说消费的物品，产生评分记录的物品是极少的。这样造成了User-Item矩阵含有大量的空值，数据极为稀疏。矩阵分解的核心思想认为用户的兴趣只受少数几个因素的影响，因此将稀疏且高维的User-Item评分矩阵分解为两个低维矩阵，即通过User、Item评分信息来学习到的用户特征矩阵P和物品特征矩阵Q，通过重构的低维矩阵预测用户对产品的评分。由于用户和物品的特征向量维度比较低，因而可以通过梯度下降(Gradient Descend)的方法高效地求解，分解示意图如下所示。

二、基本矩阵分解

　　如上所述，User-Item评分矩阵维度较高且极为稀疏，传统的奇异值分解方法只能对稠密矩阵进行分解，即不允许所分解矩阵有空值。因而，若采用奇异值分解，需要首先填充User-Item评分矩阵，显然，这样造成了两个问题。

• 其一，填充大大增加了数据量，增加了算法复杂度。
• 其二，简单粗暴的数据填充很容易造成数据失真。

　　这些问题导致了传统的SVD矩阵分解表现并不理想。之后，Simon Funk在博客上公开发表了一个只考虑已有评分记录的矩阵分解方法，称为，也就是被Yehuda Koren称为隐语义模型的矩阵分解方法。他简单地认为，既然我们的评价指标是均方根误差(Root Mean Squared Error, RMSE)，那么可以直接通过训练集中的观察值利用最小化RMSE学习用户特征矩阵P和物品特征Q，并用通过一个正则化项来避免过拟合。其需要优化的函数为

 

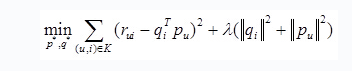
　　其中K为已有评分记录的(u,i)对集合，r_ui为用户u对物品i的真实评分，最后一项为防止过拟合的正则化项，λ为正则化系数。假设输入评分矩阵为R为M×N维矩阵，通过直接优化以上损失函数得到用户特征矩阵P(M×K)和物品特征矩阵Q(K×N)，其中K≪M,N。优化方法可以采用交叉最小二乘法或随机梯度下降方法。其评分预测方法为

 

　　其中p_u和q_i分别为用户u和物品i的特征向量，两者的内积即为所要预测的评分。

三.总结

　　R = PQ，PQ的内积来表示预测的评分，用RMSE作评价，不过不分先后顺序：在最小化RMSE约束下，来分解R矩阵，加入正则化项，防止过拟合。